###Kernel density estimate
###第一部分: 直方图
直方图是非参密度估计中最简单也是最常用到的方法.
构建直方图时,我们先将值区间切分为等间距的子区间,也叫做’bins’. 每当一个数据点落入这个子区间中的时候,在上方增加一个单元框. 它的两个重要点: 1)子区间的宽度.2)子区间的结束点.
下面选取了1956-1984年飞机尾翼跨度的数据子集(2, 22, 42, 62, 82, 102, 122, 142, 162, 182, 202 and 222).这些点在x轴上用’+’标记.
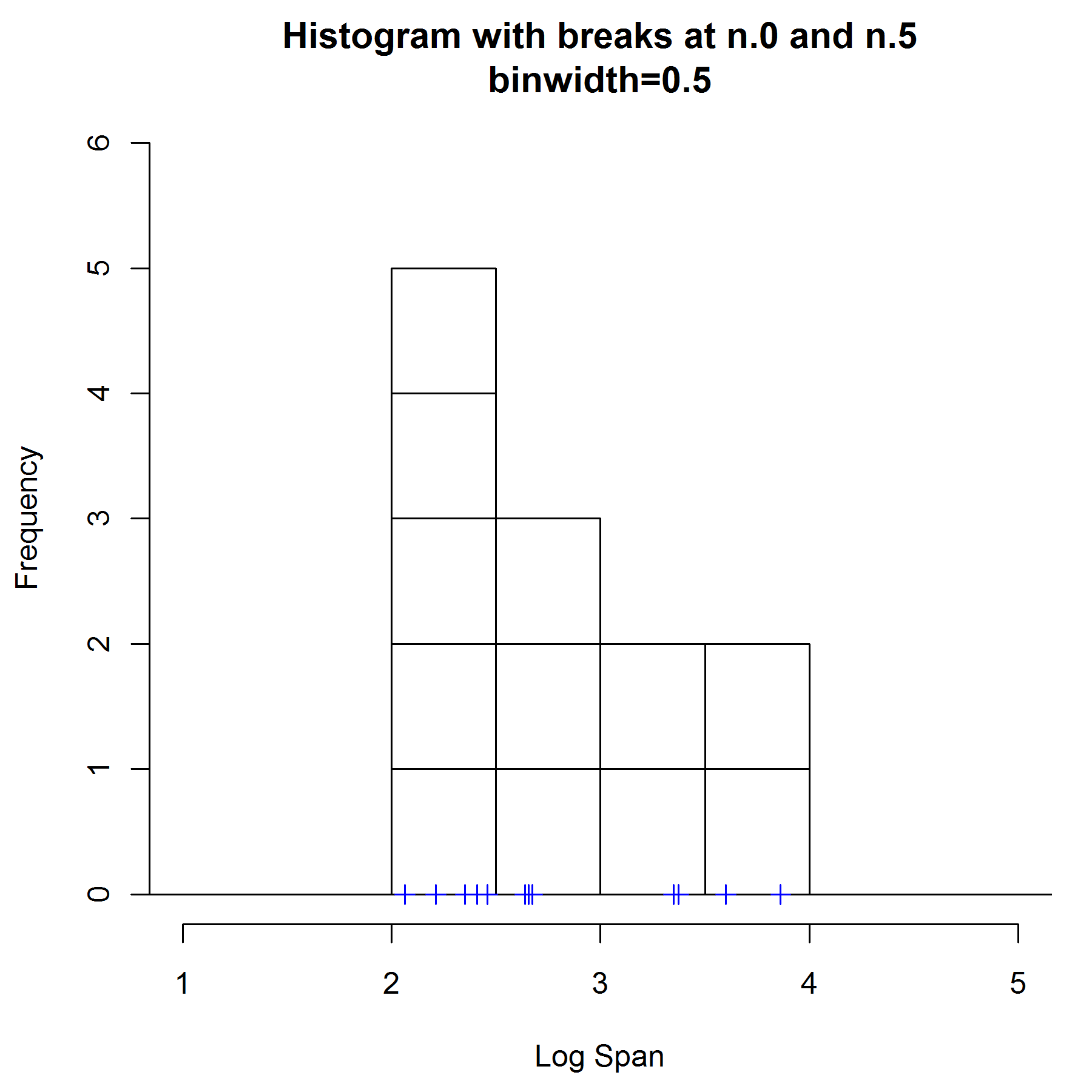
在图1中, 选择宽度为0.5, 从整数点开始放置bin,直方图的形状是单峰,并且向右倾斜.
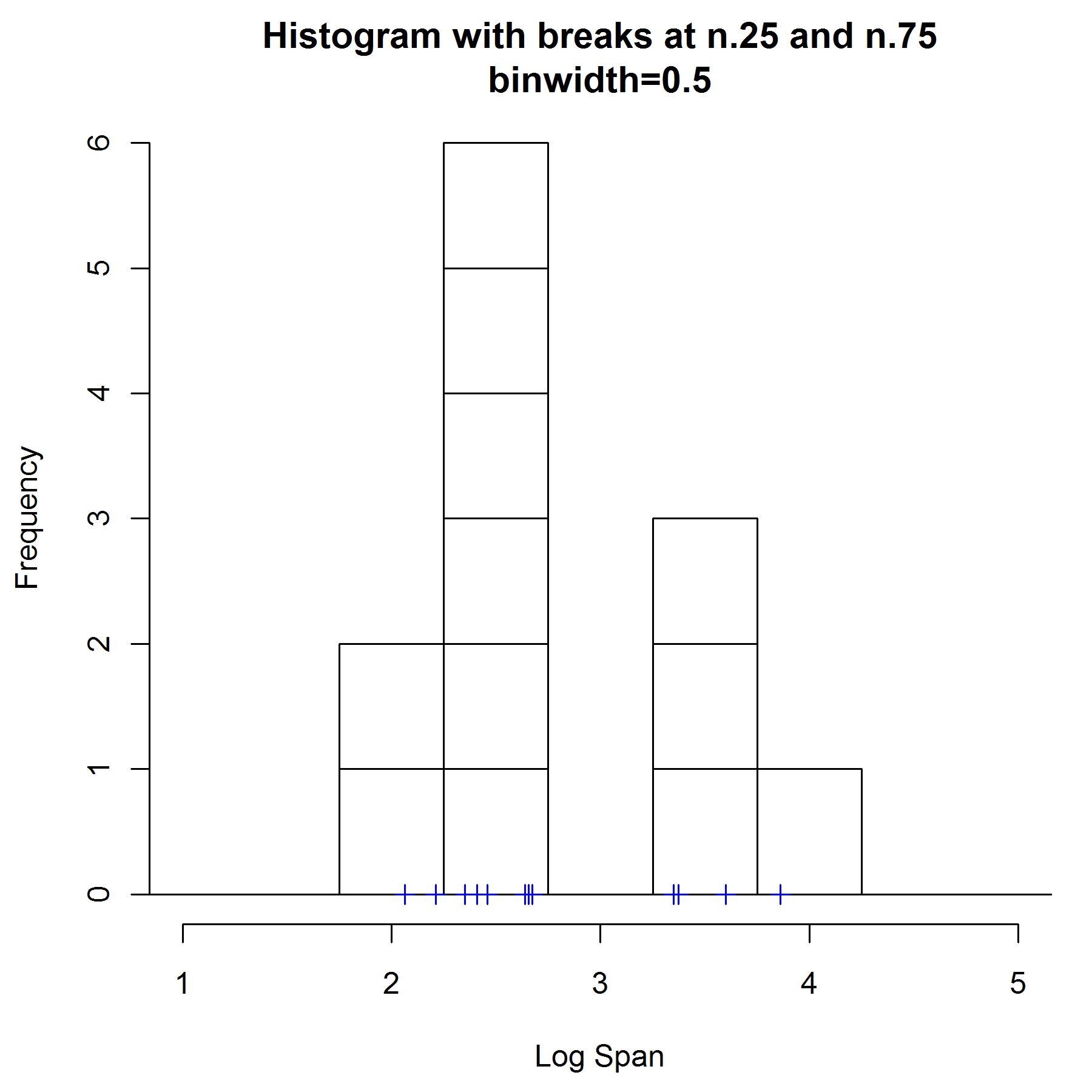
在图2中, 选择宽度为0.5, 但是从0.25处开始放置bin, 直方图的形状为双峰.
这两种bind选择,导致对该数据点的密度估计完全不同.
从上面的例子可以看出,直方图具有下面的特性:
a) 不平滑
b) 依赖bin的结束点选择
c) 依赖bind宽度
###第二部分: 密度估计方法
针对上面的问题,我们可以采用核密度估计的方法.
去掉对bin结束点的依赖,将块在数据点处进行集中.
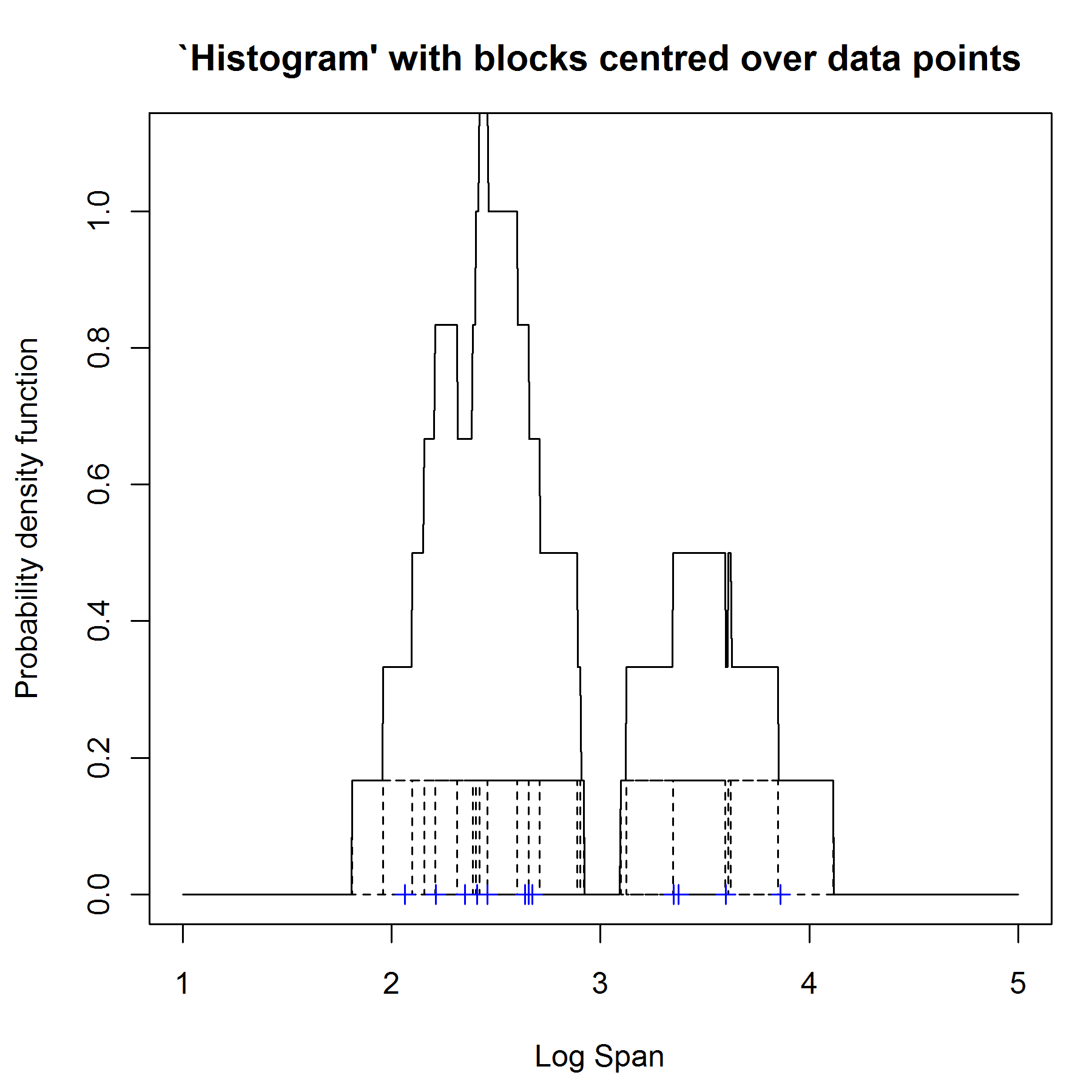
在图3中,我们在12个数据点上放置了宽度1/2,高度1/6的虚线盒子,然后将他们加起来. 我们可以从这个直方图中提取更加细微的结构,并且它表明了这个数据是双峰的.
这就是基于box kernel的密度估计,因为我们用的是离散的kernel作为building block; 如果我们用平滑的kernel作为building block,我们就可以得到一个平滑的密度估计.
虽然我们可以用这个直方图来估计这个问题,但是我们还是没能够去掉对bin宽度的依赖.
选择一个最合适的宽度值是非常重要的,它不能够太宽,也不能够太窄.如果我们选择用标准差为0.1的正态分布曲线来替代box kernel, 就可以得到一个undersmooth的估计,如下图:
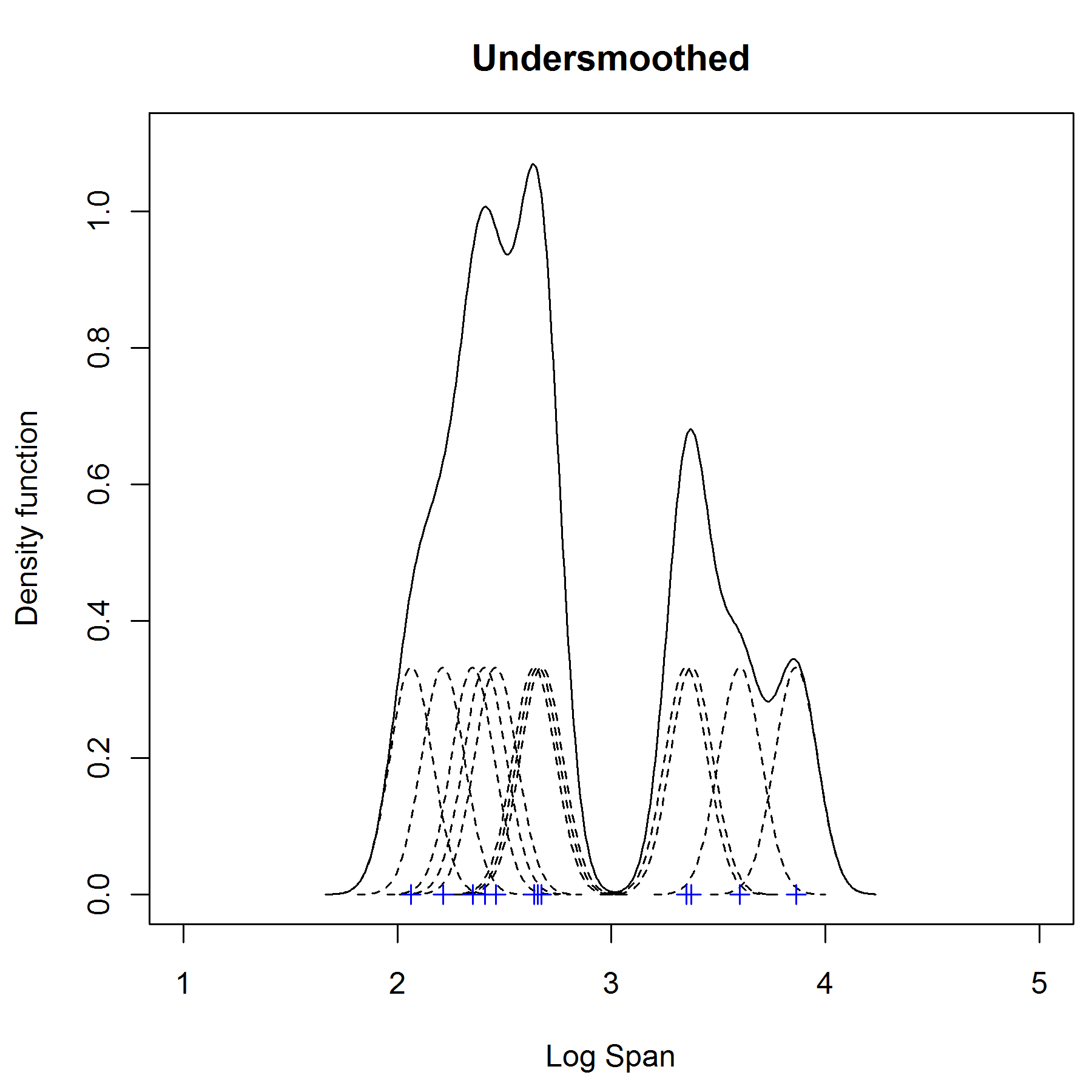
从图上可以看出,这个密度有4个峰,其中有明显的是不对的.
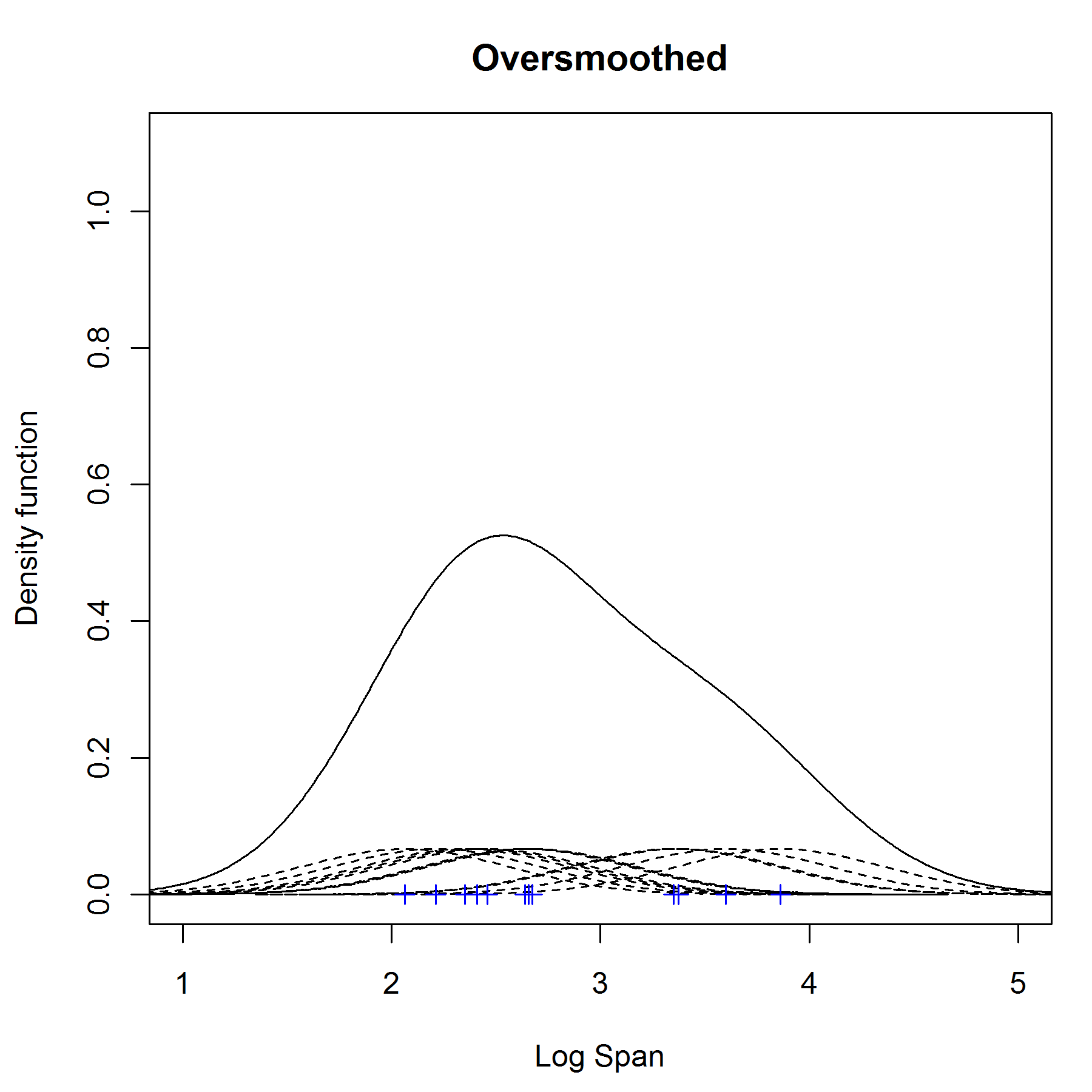
当选择了用0.5为标准差时,结果如上图, 我们得到了一个非常平坦的密度估计,这是由于选择了一个过大的宽度,导致丢失了数据的特性.
###第三部分: 如何选取合适的核来保证抽取的特征都是重要的
如何来选择一个合适的宽度呢? 通常的做法是优化一个评价标准: AMISE = Asymptotic Mean Integrated Squared Error so then optimal bandwidth = argmin AMISE i.e. the optimal bandwidth is the argument that minimises the AMISE.
通常来说, AMISE依赖于数据的真实密度(这就是要求的), 于是我们需要去极可能的估计这个密度. 这也就是说,我们选择的宽度都是去逐步逼近值.感觉上这样的估计会距离真实值很远,但实际上这些值不但保持了数据平滑,同时也能够提供出重要的特性.也就是说,能用!
对于这个数据和问题的最佳宽度是0.25, 如下图.从这个优化的平滑曲线上,可以看到数据具有两个峰.由于这些数据是经过log计算的,所以可以看出,有一些轻型的,小型的飞机被制造,主要集中在2.5(原始值12米),同样还有些大飞机,主要集中在3.5(原始值33米).
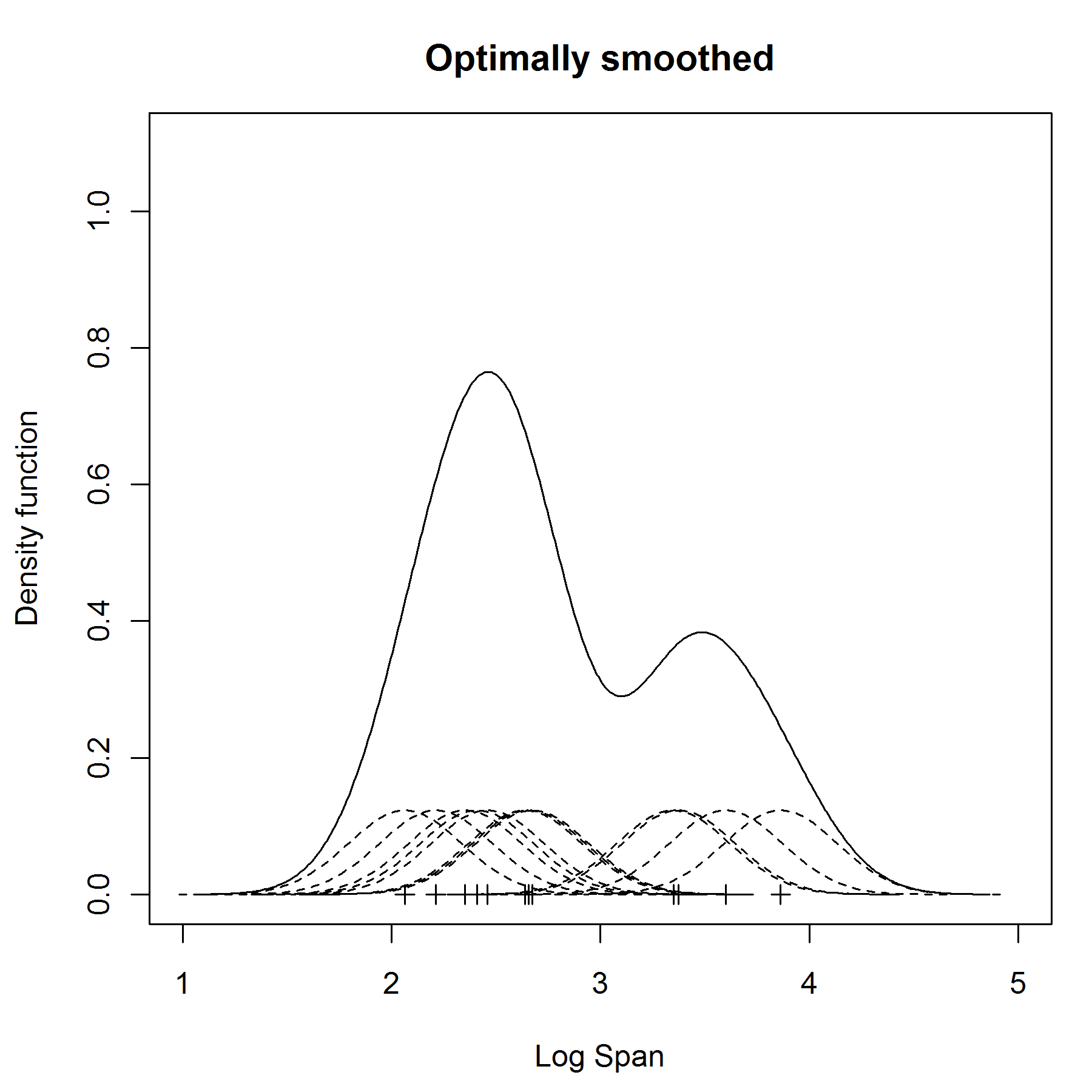
核密度估计的特点:
a) 平滑
b) 不需要bin结束点
c) 依赖bin宽度(高斯图形的宽度)
###总结
1维高斯核密度估计的方法,可以更加平滑的描述数据,用来观察数据的情况.
同样也可以扩展到多维数据的场景中, 也有了相应的用多维高斯分布来做基于密度的聚类方法.
###Reference
-
http://www.mvstat.net/tduong/research/seminars/seminar-2001-05/
-
www.mvstat.net/tduong/research/seminars/seminar-2002-05-30.pdf